How To Draw A Subgroup Lattic

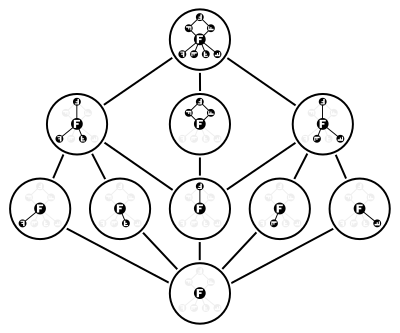
In mathematics, the lattice of subgroups of a group ${\displaystyle G}$ is the lattice whose elements are the subgroups of ${\displaystyle 1000}$ , with the partial club relation being set up inclusion. In this lattice, the bring together of two subgroups is the subgroup generated by their wedlock, and the meet of 2 subgroups is their intersection.

Instance [edit]

The dihedral group Dih₄ has x subgroups, counting itself and the trivial subgroup. Five of the eight group elements generate subgroups of order two, and the other two not-identity elements both generate the same circadian subgroup of order 4. In addition, in that location are two subgroups of the form Z_ii × Z₂, generated by pairs of order-ii elements. The lattice formed past these 10 subgroups is shown in the illustration.

This example also shows that the lattice of all subgroups of a group is not a modular lattice in general. Indeed, this particular lattice contains the forbidden "pentagon" N ₅ as a sublattice.

Properties [edit]

For any A, B, and C subgroups of a grouping with A ≤ C (A subgroup of C) so AB ∩ C = A(B ∩ C); the multiplication here is the production of subgroups. This property has been called the modular holding of groups (Aschbacher 2000) or (Dedekind'due south) modular police force (Robinson 1996, Cohn 2000). Since for two normal subgroups the product is actually the smallest subgroup containing the two, the normal subgroups form a modular lattice.

The Lattice theorem establishes a Galois connexion between the lattice of subgroups of a grouping and that of its quotients.

The Zassenhaus lemma gives an isomorphism betwixt sure combinations of quotients and products in the lattice of subgroups.

In general, at that place is no restriction on the shape of the lattice of subgroups, in the sense that every lattice is isomorphic to a sublattice of the subgroup lattice of some group. Furthermore, every finite lattice is isomorphic to a sublattice of the subgroup lattice of some finite group (Schmidt 1994, p. 9).

Characteristic lattices [edit]

Subgroups with certain properties form lattices, but other backdrop practice not.

• Normal subgroups always course a modular lattice. In fact, the essential property that guarantees that the lattice is modular is that subgroups commute with each other, i.eastward. that they are quasinormal subgroups.
• Nilpotent normal subgroups course a lattice, which is (part of) the content of Plumbing fixtures's theorem.
• In general, for any Fitting class F, both the subnormal F-subgroups and the normal F-subgroups class lattices. This includes the above with F the class of nilpotent groups, as well equally other examples such as F the class of solvable groups. A form of groups is chosen a Fitting course if it is closed under isomorphism, subnormal subgroups, and products of subnormal subgroups.
• Key subgroups form a lattice.

Still, neither finite subgroups nor torsion subgroups form a lattice: for instance, the gratis production ${\displaystyle \mathbf {Z} /2\mathbf {Z} *\mathbf {Z} /2\mathbf {Z} }$ is generated past two torsion elements, but is infinite and contains elements of infinite order.

The fact that normal subgroups form a modular lattice is a particular example of a more than general result, namely that in any Maltsev diverseness (of which groups are an example), the lattice of congruences is modular (Kearnes & Buss 2022).

Characterizing groups past their subgroup lattices [edit]

Lattice theoretic information nigh the lattice of subgroups tin can sometimes be used to infer information about the original group, an idea that goes back to the piece of work of Øystein Ore (1937, 1938). For instance, every bit Ore proved, a group is locally cyclic if and only if its lattice of subgroups is distributive. If additionally the lattice satisfies the ascending concatenation condition, then the group is cyclic.

The groups whose lattice of subgroups is a complemented lattice are called complemented groups (Zacher 1953), and the groups whose lattice of subgroups are modular lattices are chosen Iwasawa groups or modular groups (Iwasawa 1941). Lattice-theoretic characterizations of this type too exist for solvable groups and perfect groups (Suzuki 1951).

References [edit]

• Aschbacher, M. (2000). Finite Grouping Theory. Cambridge University Press. p. half-dozen. ISBN978-0-521-78675-1.
• Baer, Reinhold (1939). "The significance of the organisation of subgroups for the structure of the group". American Journal of Mathematics. The Johns Hopkins University Printing. 61 (one): ane–44. doi:x.2307/2371383. JSTOR 2371383.
• Cohn, Paul Moritz (2000). Classic algebra. Wiley. p. 248. ISBN978-0-471-87731-viii.
• Iwasawa, Kenkiti (1941), "Über die endlichen Gruppen und die Verbände ihrer Untergruppen", J. Fac. Sci. Imp. Univ. Tokyo. Sect. I., 4: 171–199, MR 0005721
• Kearnes, Keith; Kiss, Emil W. (2013). The Shape of Congruence Lattices. American Mathematical Soc. p. 3. ISBN978-0-8218-8323-five.
• Ore, Øystein (1937). "Structures and group theory. I". Duke Mathematical Journal. three (ii): 149–174. doi:10.1215/S0012-7094-37-00311-9. MR 1545977.
• Ore, Øystein (1938). "Structures and group theory. Two". Duke Mathematical Journal. iv (2): 247–269. doi:ten.1215/S0012-7094-38-00419-3. hdl:10338.dmlcz/100155. MR 1546048.
• Robinson, Derek (1996). A Form in the Theory of Groups. Springer Science & Concern Media. p. 15. ISBN978-0-387-94461-6.
• Rottlaender, Ada (1928). "Nachweis der Existenz nicht-isomorpher Gruppen von gleicher Situation der Untergruppen". Mathematische Zeitschrift. 28 (1): 641–653. doi:10.1007/BF01181188. S2CID 120596994.
• Schmidt, Roland (1994). Subgroup Lattices of Groups. Expositions in Math. Vol. 14. Walter de Gruyter. ISBN978-3-11-011213-9. Review past Ralph Freese in Balderdash. AMS 33 (iv): 487–492.
• Suzuki, Michio (1951). "On the lattice of subgroups of finite groups". Transactions of the American Mathematical Lodge. American Mathematical Society. 70 (2): 345–371. doi:x.2307/1990375. JSTOR 1990375.
• Suzuki, Michio (1956). Structure of a Group and the Structure of its Lattice of Subgroups. Berlin: Springer Verlag.
• Yakovlev, B. V. (1974). "Conditions under which a lattice is isomorphic to a lattice of subgroups of a group". Algebra and Logic. 13 (6): 400–412. doi:ten.1007/BF01462952. S2CID 119943975.
• Zacher, Giovanni (1953). "Caratterizzazione dei gruppi risolubili d'ordine finito complementati". Rendiconti del Seminario Matematico della Università di Padova. 22: 113–122. ISSN 0041-8994. MR 0057878.

External links [edit]

• PlanetMath entry on lattice of subgroups
• Example: Lattice of subgroups of the symmetric grouping S4

Source: https://en.wikipedia.org/wiki/Lattice_of_subgroups

Posted by: hatchhadmingesen.blogspot.com

Share this post