How To Draw Pca Plot For Different Group In R

Principal Component Assay for Dimensionality Reduction

Learn how to perform PCA past learning the mathematics backside the algorithm and executing it step-by-pace with Python!

In the modern age of engineering, increasing amounts of data are produced and collected. In motorcar learning, however, too much information tin be a bad affair. At a certain point, more features or dimensions can decrease a model's accuracy since there is more than data that needs to exist generalized — this is known every bit the curse of dimensionality.

Dimensionality reduction is way to reduce the complexity of a model and avert overfitting. There are two main categories of dimensionality reduction: feature option and feature extraction. Via feature selection, we select a subset of the original features, whereas in feature extraction, we derive information from the characteristic set to construct a new characteristic subspace.

In this tutorial we will explore feature extraction. In practice, feature extraction is not merely used to improve storage space or the computational efficiency of the learning algorithm, but can too better the predictive performance by reducing the expletive of dimensionality — especially if we are working with non-regularized models.

Specifically, we volition discuss the Main Component Assay (PCA) algorithm used to compress a dataset onto a lower-dimensional characteristic subspace with the goal of maintaining almost of the relevant information. We will explore:

The concepts and mathematics behind PCA
How to execute PCA step-past-step from scratch using Python
How to execute PCA using the Python library scikit-learn

Let'south become started!

This tutorial is adapted from Office 2 of Next Tech's Python Machine Learning serial, which takes you through motorcar learning and deep learning algorithms with Python from 0 to 100. It includes an in-browser sandboxed environment with all the necessary software and libraries pre-installed, and projects using public datasets. Y'all can get started for gratuitous here !

Introduction to Principal Component Analysis

Main Component Analysis (PCA) is an unsupervised linear transformation technique that is widely used across different fields, near prominently for feature extraction and dimensionality reduction. Other pop applications of PCA include exploratory data analyses and de-noising of signals in stock market trading, and the analysis of genome data and cistron expression levels in the field of bioinformatics.

PCA helps united states of america to identify patterns in information based on the correlation between features. In a nutshell, PCA aims to discover the directions of maximum variance in loftier-dimensional data and projects it onto a new subspace with equal or fewer dimensions than the original one.

The orthogonal axes (principal components) of the new subspace can be interpreted as the directions of maximum variance given the constraint that the new feature axes are orthogonal to each other, equally illustrated in the following figure:

In the preceding figure, x1 and x2 are the original feature axes, and PC1 and PC2 are the principal components.

If we use PCA for dimensionality reduction, we construct a d ten k–dimensional transformation matrix West that allows us to map a sample vector 10 onto a new chiliad–dimensional feature subspace that has fewer dimensions than the original d–dimensional feature space:

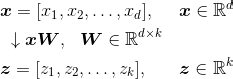
As a outcome of transforming the original d-dimensional data onto this new k-dimensional subspace (typically grand ≪ d), the first chief component will take the largest possible variance, and all consequent principal components will have the largest variance given the constraint that these components are uncorrelated (orthogonal) to the other principal components — even if the input features are correlated, the resulting main components will be mutually orthogonal (uncorrelated).

Annotation that the PCA directions are highly sensitive to data scaling, and we need to standardize the features prior to PCA if the features were measured on dissimilar scales and we desire to assign equal importance to all features.

Before looking at the PCA algorithm for dimensionality reduction in more item, let's summarize the approach in a few simple steps:

Standardize the d-dimensional dataset.
Construct the covariance matrix.
Decompose the covariance matrix into its eigenvectors and eigenvalues.
Sort the eigenvalues by decreasing order to rank the corresponding eigenvectors.
Select thou eigenvectors which correspond to the thou largest eigenvalues, where thou is the dimensionality of the new feature subspace (k ≤ d).
Construct a projection matrix W from the "top" k eigenvectors.
Transform the d-dimensional input dataset Ten using the projection matrix Due west to obtain the new thousand-dimensional feature subspace.

Let's perform a PCA stride by step, using Python every bit a learning do. Then, nosotros will come across how to perform a PCA more than conveniently using scikit-learn.

Extracting the Principal Components Stride Past Pace

Nosotros will exist using the Wine dataset from The UCI Auto Learning Repository in our example. This dataset consists of 178 vino samples with 13 features describing their different chemical backdrop. You can find out more hither.

In this department we will tackle the first four steps of a PCA; later we volition become over the terminal three. Y'all can follow along with the code in this tutorial by using a Next Tech sandbox, which has all the necessary libraries pre-installed, or if you lot'd adopt, you tin run the snippets in your own local environment.

In one case your sandbox loads, we will outset by loading the Vino dataset directly from the repository:

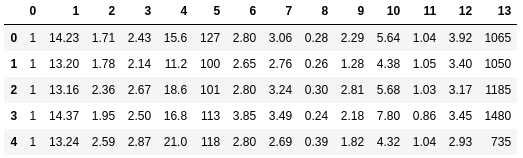
Next, we will process the Wine data into separate training and test sets — using a 70:30 split — and standardize it to unit variance:

After completing the mandatory preprocessing, let's advance to the second pace: constructing the covariance matrix. The symmetric d 10 d-dimensional covariance matrix, where d is the number of dimensions in the dataset, stores the pairwise covariances between the different features. For case, the covariance betwixt two features x_j and x_k on the population level can be calculated via the following equation:

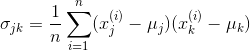
Hither, μ_j and μ_k are the sample means of features j and thou, respectively.

Annotation that the sample ways are zero if we standardized the dataset. A positive covariance between two features indicates that the features increment or decrease together, whereas a negative covariance indicates that the features vary in opposite directions. For case, the covariance matrix of three features can and so exist written equally follows (note that Σ stands for the Greek uppercase letter sigma, which is not to be confused with the sum symbol):

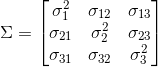
The eigenvectors of the covariance matrix represent the principal components (the directions of maximum variance), whereas the corresponding eigenvalues will define their magnitude. In the case of the Wine dataset, nosotros would obtain 13 eigenvectors and eigenvalues from the 13 10 13-dimensional covariance matrix.

Now, for our tertiary stride, let's obtain the eigenpairs of the covariance matrix. An eigenvector v satisfies the post-obit condition:

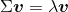
Here, λ is a scalar: the eigenvalue. Since the manual computation of eigenvectors and eigenvalues is a somewhat tiresome and elaborate task, we will employ the linalg.eig office from NumPy to obtain the eigenpairs of the Wine covariance matrix:

Using the numpy.cov function, nosotros computed the covariance matrix of the standardized preparation dataset. Using the linalg.eig office, we performed the eigendecomposition, which yielded a vector (eigen_vals) consisting of xiii eigenvalues and the corresponding eigenvectors stored as columns in a xiii x 13-dimensional matrix (eigen_vecs).

Total and Explained Variance

Since we desire to reduce the dimensionality of our dataset past compressing it onto a new characteristic subspace, we only select the subset of the eigenvectors (master components) that contains most of the information (variance). The eigenvalues define the magnitude of the eigenvectors, and then we have to sort the eigenvalues by decreasing magnitude; we are interested in the top yard eigenvectors based on the values of their corresponding eigenvalues.

But before nosotros collect those k most informative eigenvectors, permit's plot the variance explained ratios of the eigenvalues. The variance explained ratio of an eigenvalue λ_j is but the fraction of an eigenvalue λ_j and the total sum of the eigenvalues:

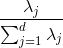
Using the NumPy cumsum office, we tin can then summate the cumulative sum of explained variances, which nosotros will then plot via matplotlib'south step function:

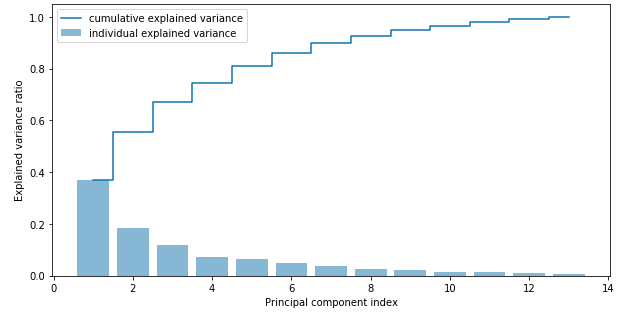
The resulting plot indicates that the first principal component alone accounts for approximately 40% of the variance. Also, we tin see that the showtime two principal components combined explain nearly threescore% of the variance in the dataset.

Feature Transformation

After we have successfully decomposed the covariance matrix into eigenpairs, permit'due south at present go on with the final iii steps of PCA to transform the Vino dataset onto the new master component axes.

We will sort the eigenpairs by descending order of the eigenvalues, construct a projection matrix from the selected eigenvectors, and use the projection matrix to transform the data onto the lower-dimensional subspace.

Nosotros start by sorting the eigenpairs past decreasing order of the eigenvalues:

Side by side, we collect the 2 eigenvectors that correspond to the two largest eigenvalues, to capture about lx% of the variance in this dataset. Note that we only chose two eigenvectors for the purpose of illustration, since nosotros are going to plot the data via a two-dimensional scatter plot subsequently in this subsection. In practice, the number of chief components has to exist adamant by a merchandise-off between computational efficiency and the operation of the classifier:

          [Out:]
Matrix Due west:
            [[-0.13724218  0.50303478]
            [ 0.24724326  0.16487119]
            [-0.02545159  0.24456476]
            [ 0.20694508 -0.11352904]
            [-0.15436582  0.28974518]
            [-0.39376952  0.05080104]
            [-0.41735106 -0.02287338]
            [ 0.30572896  0.09048885]
            [-0.30668347  0.00835233]
            [ 0.07554066  0.54977581]
            [-0.32613263 -0.20716433]
            [-0.36861022 -0.24902536]
            [-0.29669651  0.38022942]]

By executing the preceding lawmaking, we have created a 13 x 2-dimensional projection matrix W from the top ii eigenvectors.

Using the projection matrix, we can at present transform a sample x (represented as a ane x 13-dimensional row vector) onto the PCA subspace (the principal components one and two) obtaining ten′ , now a two-dimensional sample vector consisting of 2 new features:

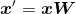
Similarly, we can transform the entire 124 10 xiii-dimensional training dataset onto the 2 principal components by calculating the matrix dot product:

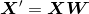
Lastly, let's visualize the transformed Vino training ready, now stored equally an 124 10 ii-dimensional matrix, in a two-dimensional scatterplot:

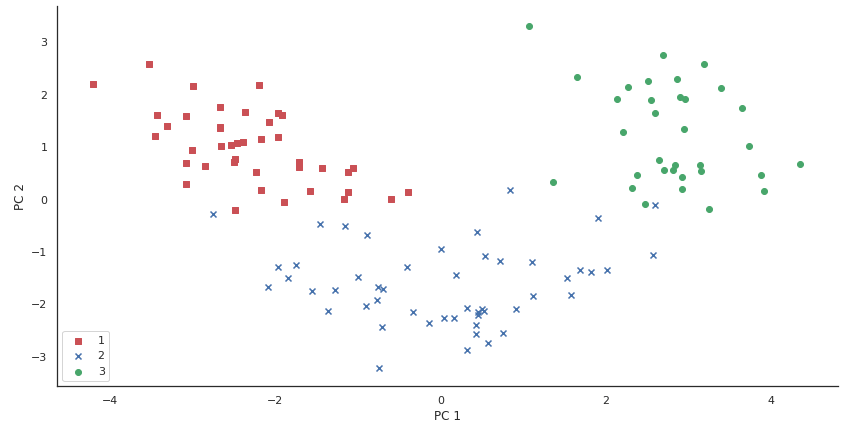
Every bit we can see in the resulting plot, the data is more spread along the ten-axis — the first principal component — than the 2d principal component (y-axis), which is consistent with the explained variance ratio plot that we created previously. However, we tin can intuitively encounter that a linear classifier will likely be able to separate the classes well.

Although we encoded the class label information for the purpose of illustration in the preceding scatter plot, we accept to proceed in mind that PCA is an unsupervised technique that does not utilise whatever form characterization information.

PCA in scikit-learn

Although the verbose arroyo in the previous subsection helped us to follow the inner workings of PCA, we will now discuss how to use the PCA class implemented in scikit-acquire. The PCA form is another one of scikit-learn'south transformer classes, where we first fit the model using the preparation data before we transform both the training data and the exam dataset using the same model parameters.

Allow's utilize the PCA class on the Wine grooming dataset, allocate the transformed samples via logistic regression:

Now, using a custom plot_decision_regions office, we will visualize the decision regions:

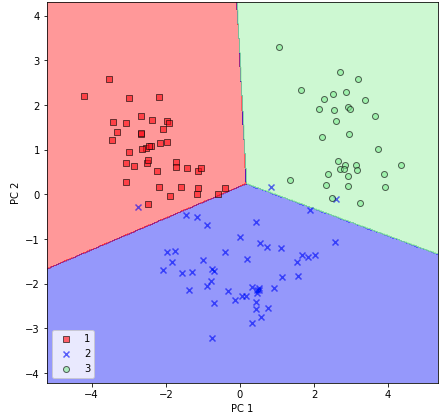
By executing the preceding lawmaking, we should now see the decision regions for the preparation data reduced to two chief component axes.

For the sake of abyss, let's plot the conclusion regions of the logistic regression on the transformed exam dataset besides to see if information technology tin separate the classes well:

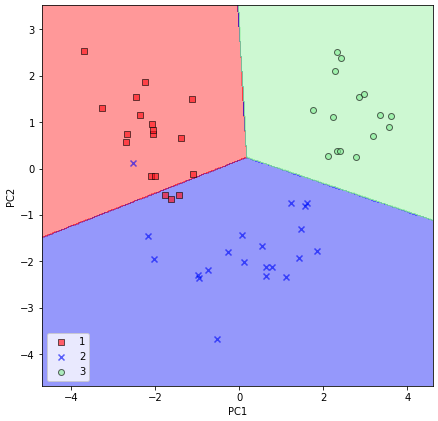
After we plotted the decision regions for the examination set by executing the preceding code, we can meet that logistic regression performs quite well on this small two-dimensional feature subspace and only misclassifies very few samples in the exam dataset.

If we are interested in the explained variance ratios of the dissimilar master components, we can merely initialize the PCA course with the n_components parameter set up to None, so all chief components are kept and the explained variance ratio can then be accessed via the explained_variance_ratio_ attribute:

Notation that we fix n_components=None when we initialized the PCA class so that it will render all principal components in a sorted lodge instead of performing a dimensionality reduction.

I hope you enjoyed this tutorial on main component analysis for dimensionality reduction! We covered the mathematics behind the PCA algorithm, how to perform PCA step-by-step with Python, and how to implement PCA using scikit-acquire. Other techniques for dimensionality reduction are Linear Discriminant Assay (LDA) and Kernel PCA (used for not-linearly separable data).

These other techniques and more topics to improve model performance, such as data preprocessing, model evaluation, hyperparameter tuning, and ensemble learning techniques are covered in Next Tech'southward Python Car Learning (Role 2) grade.

You can get started here for gratuitous!